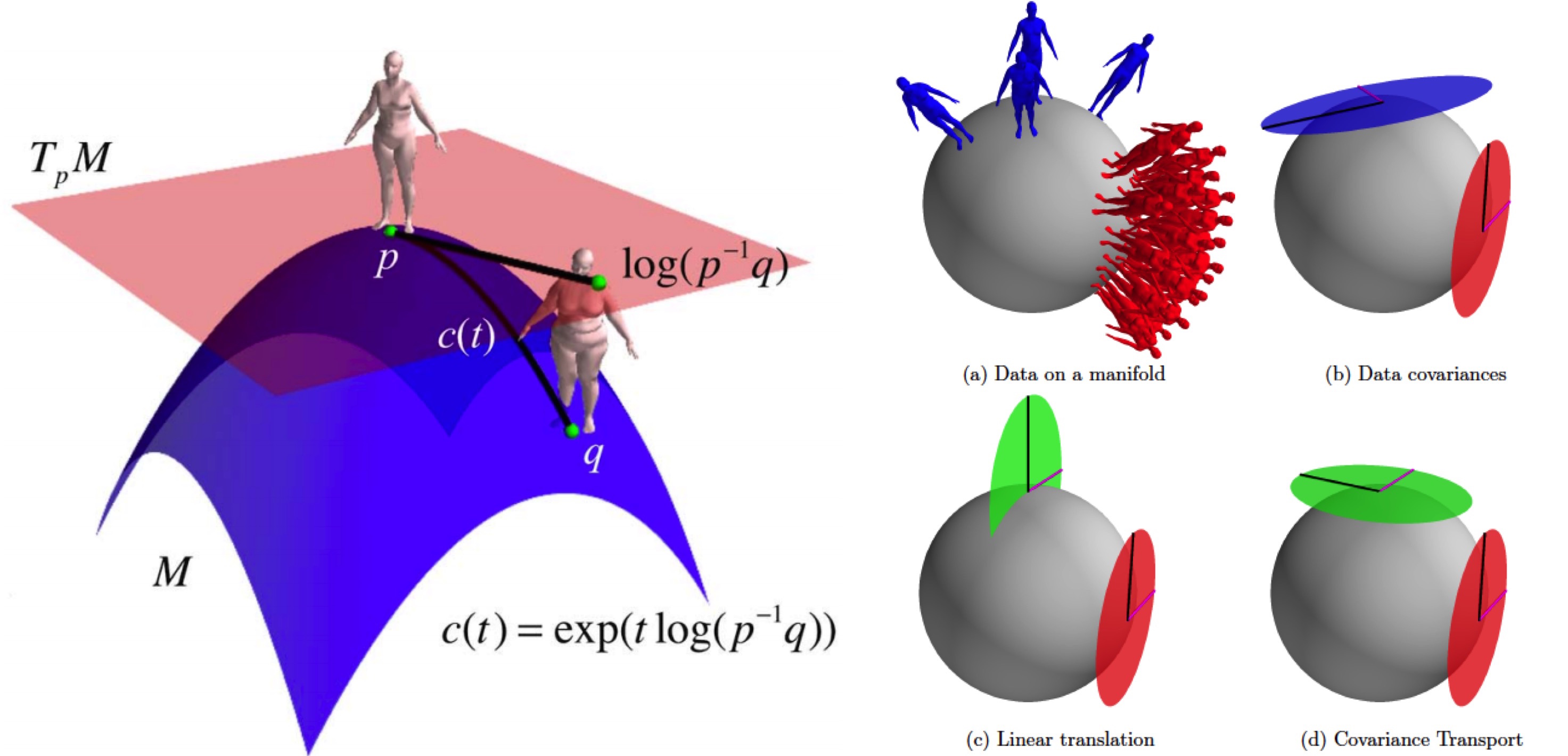
Statistics on manifolds. Left: body shape represented as deformations where the deformations lie on a manifold. Right: transporting statistics on a manifold. Here we use the statistics of female shape to regularize the shape of men using covariance transport.
Statistics is traditionally concerned with data in a Euclidean space, relying on the linear structure and the distances associated with such a space; this renders it inappropriate for nonlinear spaces. Statistics can, however, be generalized to nonlinear manifolds. Moreover, by respecting the underlying geometry, the statistical models result in not only more effective analysis but also consistent synthesis. We go beyond previous work on statistics on manifolds by showing how, even on these curved spaces, problems related to modeling a class from scarce data can be dealt with by leveraging information from related classes residing in di fferent regions of the space. We show the usefulness of our approach with 3D shape deformations.
Three-dimensional object shape is commonly represented in terms of deformations of a triangular mesh from an exemplar shape. Existing models, however, are based on a Euclidean representation of shape deformations. In contrast, we argue that shape has a manifold structure: For example, summing the shape deformations for two people does not necessarily yield a deformation corresponding to a valid human shape, nor does the Euclidean difference of these two deformations provide a meaningful measure of shape dissimilarity. Consequently, we define a novel manifold for shape representation, with emphasis on body shapes, using a new Lie group of deformations. This has several advantages. First we define triangle deformations exactly, removing non-physical deformations and redundant degrees of freedom common to previous methods. Second, the Riemannian structure of Lie Bodies enables a more meaningful definition of body shape similarity by measuring distance between bodies on the manifold of body shape deformations. Third, the group structure allows the valid composition of deformations. This is important for models that factor body shape deformations into multiple causes or represent shape as a linear combination of basis shapes. Finally, body shape variation is modeled using statistics on manifolds. Instead of modeling Euclidean shape variation with Principal Component Analysis we capture shape variation on the manifold using Principal Geodesic Analysis. Our experiments show consistent visual and quantitative advantages of Lie Bodies over traditional Euclidean models of shape deformation and our representation can be easily incorporated into existing methods.
In modeling 3D shapes we often face a situation of limited data. Can we leverage information about other shapes to help model a new one? To address this, we combine transfer learning and statistics on manifolds. In particular, we consider, for manifold-valued data, transfer learning of tangent-space models such as Gaussians distributions, PCA, regression, or classifiers. Though one would hope to simply use ordinary Euclidean transfer learning ideas, the manifold structure prevents it. We overcome this by basing our method on inner-product-preserving parallel transport, a well-known tool widely used in other problems of statistics on manifolds in computer vision. At first, this straightforward idea seems to suffer from an obvious shortcoming: Transporting large datasets is prohibitively expensive, hindering scalability. Fortunately, with our approach, we never transport data. Rather, we show how the statistical models themselves can be transported, and prove that for the tangent-space models above, the transport “commutes” with learning. Consequently, our compact framework, applicable to a large class of manifolds, is not restricted by the size of either the training or test sets. We demonstrate the approach by transferring PCA and logistic-regression models of real-world data involving 3D shapes and image descriptors.
